Class implements G-Means clustering algorithm. More...

Public Member Functions
def	__init__ (self, data, k_init=1, ccore=True, **kwargs)
	Initializes G-Means algorithm. More...

def	process (self)
	Performs cluster analysis in line with rules of G-Means algorithm. More...

def	predict (self, points)
	Calculates the closest cluster to each point. More...

def	get_clusters (self)
	Returns list of allocated clusters, each cluster contains indexes of objects in list of data. More...

def	get_centers (self)
	Returns list of centers of allocated clusters. More...

def	get_total_wce (self)
	Returns sum of metric errors that depends on metric that was used for clustering (by default SSE - Sum of Squared Errors). More...

def	get_cluster_encoding (self)
	Returns clustering result representation type that indicate how clusters are encoded. More...

Detailed Description

Class implements G-Means clustering algorithm.

The G-means algorithm starts with a small number of centers, and grows the number of centers. Each iteration of the G-Means algorithm splits into two those centers whose data appear not to come from a Gaussian distribution. G-means repeatedly makes decisions based on a statistical test for the data assigned to each center.

Implementation based on the paper [17].

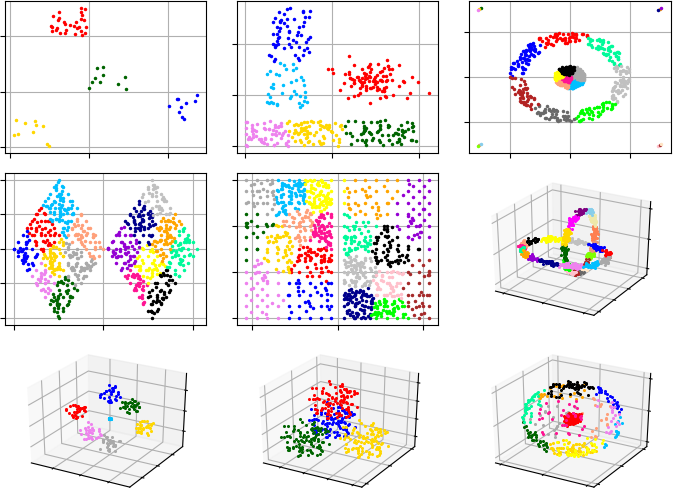
G-Means clustering results on most common data-sets.

Example #1. In this example, G-Means starts analysis from single cluster.

from pyclustering.cluster import cluster_visualizer
from pyclustering.cluster.gmeans import gmeans
from pyclustering.utils import read_sample
from pyclustering.samples.definitions import FCPS_SAMPLES
 
# Read sample 'Lsun' from file.
sample = read_sample(FCPS_SAMPLES.SAMPLE_LSUN)
 
# Create instance of G-Means algorithm. By default the algorithm starts search from a single cluster.
gmeans_instance = gmeans(sample).process()
 
# Extract clustering results: clusters and their centers
clusters = gmeans_instance.get_clusters()
centers = gmeans_instance.get_centers()
 
# Print total sum of metric errors
print("Total WCE:", gmeans_instance.get_total_wce())
 
# Visualize clustering results
visualizer = cluster_visualizer()
visualizer.append_clusters(clusters, sample)
visualizer.show()

Example #2. Sometimes G-Means might find local optimum. repeat value can be used to increase probability to find global optimum. Argument repeat defines how many times K-Means clustering with K-Means++ initialization should be run in order to find optimal clusters.

# Read sample 'Tetra' from file.
sample = read_sample(FCPS_SAMPLES.SAMPLE_TETRA)
 
# Create instance of G-Means algorithm. By default algorithm start search from single cluster.
gmeans_instance = gmeans(sample, repeat=10).process()
 
# Extract clustering results: clusters and their centers
clusters = gmeans_instance.get_clusters()
 
# Visualize clustering results
visualizer = cluster_visualizer()
visualizer.append_clusters(clusters, sample)
visualizer.show()

In case of requirement to have labels instead of default representation of clustering results CLUSTER_INDEX_LIST_SEPARATION:

from pyclustering.cluster.gmeans import gmeans
from pyclustering.cluster.encoder import type_encoding, cluster_encoder
from pyclustering.samples.definitions import SIMPLE_SAMPLES
from pyclustering.utils import read_sample
 
data = read_sample(SIMPLE_SAMPLES.SAMPLE_SIMPLE1)
 
gmeans_instance = gmeans(data).process()
clusters = gmeans_instance.get_clusters()
 
# Change cluster representation from default to labeling.
encoder = cluster_encoder(type_encoding.CLUSTER_INDEX_LIST_SEPARATION, clusters, data)
encoder.set_encoding(type_encoding.CLUSTER_INDEX_LABELING)
labels = encoder.get_clusters()
 
print(labels)   # Display labels

There is an output of the code above:

[0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

Definition at line 25 of file gmeans.py.

Constructor & Destructor Documentation

◆ init()

def pyclustering.cluster.gmeans.gmeans.__init__	(		self,
			data,
			k_init = `1`,
			ccore = `True`,
		**	kwargs
	)

Initializes G-Means algorithm.

Parameters

[in]	data	(array_like): Input data that is presented as array of points (objects), each point should be represented by array_like data structure.
[in]	k_init	(uint): Initial amount of centers (by default started search from 1).
[in]	ccore	(bool): Defines whether CCORE library (C/C++ part of the library) should be used instead of Python code.
[in]	**kwargs	Arbitrary keyword arguments (available arguments: `tolerance`, `repeat`, `k_max`, `random_state`).

Keyword Args:

tolerance (double): tolerance (double): Stop condition for each K-Means iteration: if maximum value of change of centers of clusters is less than tolerance than algorithm will stop processing.
repeat (unit): How many times K-Means should be run to improve parameters (by default is 3). With larger 'repeat' values suggesting higher probability of finding global optimum.
k_max (uint): Maximum amount of cluster that might be allocated. The argument is considered as a stop condition. When the maximum amount is reached then algorithm stops processing. By default the maximum amount of clusters is not restricted (k_max is -1).
random_state (int): Seed for random state (by default is None, current system time is used).

Definition at line 109 of file gmeans.py.

Member Function Documentation

◆ get_centers()

def pyclustering.cluster.gmeans.gmeans.get_centers ( self )

Returns list of centers of allocated clusters.

Returns: (array_like) Allocated centers.

See also: process(); get_clusters()

Definition at line 231 of file gmeans.py.

◆ get_cluster_encoding()

def pyclustering.cluster.gmeans.gmeans.get_cluster_encoding ( self )

Returns clustering result representation type that indicate how clusters are encoded.

Returns: (type_encoding) Clustering result representation.

See also: get_clusters()

Definition at line 258 of file gmeans.py.

◆ get_clusters()

def pyclustering.cluster.gmeans.gmeans.get_clusters ( self )

Returns list of allocated clusters, each cluster contains indexes of objects in list of data.

Returns: (array_like) Allocated clusters.

See also: process(); get_centers()

Definition at line 218 of file gmeans.py.

Referenced by pyclustering.samples.answer_reader.get_cluster_lengths(), and pyclustering.cluster.optics.optics.process().

◆ get_total_wce()

def pyclustering.cluster.gmeans.gmeans.get_total_wce ( self )

Returns sum of metric errors that depends on metric that was used for clustering (by default SSE - Sum of Squared Errors).

Sum of metric errors is calculated using distance between point and its center:

\[error=\sum_{i=0}^{N}distance(x_{i}-center(x_{i}))\]

See also: process(); get_clusters()

Definition at line 244 of file gmeans.py.

◆ predict()

def pyclustering.cluster.gmeans.gmeans.predict	(	self,
		points
	)

Calculates the closest cluster to each point.

Parameters

[in] points (array_like): Points for which closest clusters are calculated.

Returns: (list) List of closest clusters for each point. Each cluster is denoted by index. Return empty collection if 'process()' method was not called.

Definition at line 194 of file gmeans.py.

◆ process()

def pyclustering.cluster.gmeans.gmeans.process ( self )

Performs cluster analysis in line with rules of G-Means algorithm.

Returns: (gmeans) Returns itself (G-Means instance).

See also: get_clusters(); get_centers()

Definition at line 150 of file gmeans.py.

Referenced by pyclustering.cluster.gmeans.gmeans.get_cluster_encoding().

The documentation for this class was generated from the following file:

pyclustering/cluster/gmeans.py

Public Member Functions