Class represents clustering algorithm X-Means. More...

Public Member Functions
def	__init__ (self, data, initial_centers=None, kmax=20, tolerance=0.001, criterion=splitting_type.BAYESIAN_INFORMATION_CRITERION, ccore=True, **kwargs)
	Constructor of clustering algorithm X-Means. More...

def	process (self)
	Performs cluster analysis in line with rules of X-Means algorithm. More...

def	predict (self, points)
	Calculates the closest cluster to each point. More...

def	get_clusters (self)
	Returns list of allocated clusters, each cluster contains indexes of objects in list of data. More...

def	get_centers (self)
	Returns list of centers for allocated clusters. More...

def	get_cluster_encoding (self)
	Returns clustering result representation type that indicate how clusters are encoded. More...

def	get_total_wce (self)
	Returns sum of Euclidean Squared metric errors (SSE - Sum of Squared Errors). More...

Detailed Description

Class represents clustering algorithm X-Means.

X-means clustering method starts with the assumption of having a minimum number of clusters, and then dynamically increases them. X-means uses specified splitting criterion to control the process of splitting clusters. Method K-Means++ can be used for calculation of initial centers.

CCORE implementation of the algorithm uses thread pool to parallelize the clustering process.

Here example how to perform cluster analysis using X-Means algorithm:

from pyclustering.cluster import cluster_visualizer
from pyclustering.cluster.xmeans import xmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
from pyclustering.utils import read_sample
from pyclustering.samples.definitions import SIMPLE_SAMPLES
 
# Read sample 'simple3' from file.
sample = read_sample(SIMPLE_SAMPLES.SAMPLE_SIMPLE3)
 
# Prepare initial centers - amount of initial centers defines amount of clusters from which X-Means will
# start analysis.
amount_initial_centers = 2
initial_centers = kmeans_plusplus_initializer(sample, amount_initial_centers).initialize()
 
# Create instance of X-Means algorithm. The algorithm will start analysis from 2 clusters, the maximum
# number of clusters that can be allocated is 20.
xmeans_instance = xmeans(sample, initial_centers, 20)
xmeans_instance.process()
 
# Extract clustering results: clusters and their centers
clusters = xmeans_instance.get_clusters()
centers = xmeans_instance.get_centers()
 
# Print total sum of metric errors
print("Total WCE:", xmeans_instance.get_total_wce())
 
# Visualize clustering results
visualizer = cluster_visualizer()
visualizer.append_clusters(clusters, sample)
visualizer.append_cluster(centers, None, marker='*', markersize=10)
visualizer.show()

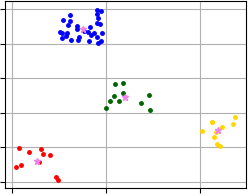
Visualization of clustering results that were obtained using code above and where X-Means algorithm allocates four clusters.

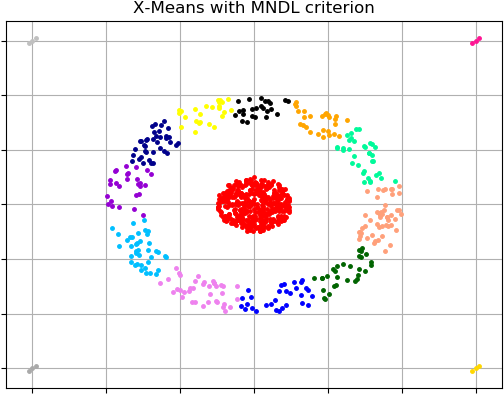
Fig. 1. X-Means clustering results (data 'Simple3').

By default X-Means clustering algorithm uses Bayesian Information Criterion (BIC) to approximate the correct number of clusters. There is an example where another criterion Minimum Noiseless Description Length (MNDL) is used in order to find optimal amount of clusters:

from pyclustering.cluster import cluster_visualizer
from pyclustering.cluster.xmeans import xmeans, splitting_type
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
from pyclustering.utils import read_sample
from pyclustering.samples.definitions import FCPS_SAMPLES
 
# Read sample 'Target'.
sample = read_sample(FCPS_SAMPLES.SAMPLE_TARGET)
 
# Prepare initial centers - amount of initial centers defines amount of clusters from which X-Means will start analysis.
random_seed = 1000
amount_initial_centers = 3
initial_centers = kmeans_plusplus_initializer(sample, amount_initial_centers, random_state=random_seed).initialize()
 
# Create instance of X-Means algorithm with MNDL splitting criterion.
xmeans_mndl = xmeans(sample, initial_centers, 20, splitting_type=splitting_type.MINIMUM_NOISELESS_DESCRIPTION_LENGTH, random_state=random_seed)
xmeans_mndl.process()
 
# Extract X-Means MNDL clustering results.
mndl_clusters = xmeans_mndl.get_clusters()
 
# Visualize clustering results.
visualizer = cluster_visualizer(titles=['X-Means with MNDL criterion'])
visualizer.append_clusters(mndl_clusters, sample)
visualizer.show()

Fig. 2. X-Means MNDL clustering results (data 'Target').

As in many others algorithms, it is possible to specify metric that should be used for cluster analysis, for example, Chebyshev distance metric:

# Create instance of X-Means algorithm with Chebyshev distance metric.
chebyshev_metric = distance_metric(type_metric.CHEBYSHEV)
xmeans_instance = xmeans(sample, initial_centers, max_clusters_amount, metric=chebyshev_metric).process()

See also: center_initializer

Definition at line 63 of file xmeans.py.

Constructor & Destructor Documentation

◆ init()

def pyclustering.cluster.xmeans.xmeans.__init__	(		self,
			data,
			initial_centers = `None`,
			kmax = `20`,
			tolerance = `0.001`,
			criterion = `splitting_type.BAYESIAN_INFORMATION_CRITERION`,
			ccore = `True`,
		**	kwargs
	)

Constructor of clustering algorithm X-Means.

Parameters

[in]	data	(array_like): Input data that is presented as list of points (objects), each point should be represented by list or tuple.
[in]	initial_centers	(list): Initial coordinates of centers of clusters that are represented by list: `[center1, center2, ...]`, if it is not specified then X-Means starts from the random center.
[in]	kmax	(uint): Maximum number of clusters that can be allocated.
[in]	tolerance	(double): Stop condition for each iteration: if maximum value of change of centers of clusters is less than tolerance than algorithm will stop processing.
[in]	criterion	(splitting_type): Type of splitting creation (by default `splitting_type.BAYESIAN_INFORMATION_CRITERION`).
[in]	ccore	(bool): Defines if C++ pyclustering library should be used instead of Python implementation.
[in]	**kwargs	Arbitrary keyword arguments (available arguments: `repeat`, `random_state`, `metric`, `alpha`, `beta`).

Keyword Args:

repeat (unit): How many times K-Means should be run to improve parameters (by default is 1). With larger repeat values suggesting higher probability of finding global optimum.
random_state (int): Seed for random state (by default is None, current system time is used).
metric (distance_metric): Metric that is used for distance calculation between two points (by default euclidean square distance).
alpha (double): Parameter distributed [0.0, 1.0] for alpha probabilistic bound \(Q\left(\alpha\right)\). The parameter is used only in case of MNDL splitting criterion, in all other cases this value is ignored.
beta (double): Parameter distributed [0.0, 1.0] for beta probabilistic bound \(Q\left(\beta\right)\). The parameter is used only in case of MNDL splitting criterion, in all other cases this value is ignored.

Definition at line 155 of file xmeans.py.

Member Function Documentation

◆ get_centers()

def pyclustering.cluster.xmeans.xmeans.get_centers ( self )

Returns list of centers for allocated clusters.

Returns: (list) List of centers for allocated clusters.

See also: process(); get_clusters(); get_total_wce()

Definition at line 329 of file xmeans.py.

◆ get_cluster_encoding()

def pyclustering.cluster.xmeans.xmeans.get_cluster_encoding ( self )

Returns clustering result representation type that indicate how clusters are encoded.

Returns: (type_encoding) Clustering result representation.

See also: get_clusters()

Definition at line 344 of file xmeans.py.

◆ get_clusters()

def pyclustering.cluster.xmeans.xmeans.get_clusters ( self )

Returns list of allocated clusters, each cluster contains indexes of objects in list of data.

Returns: (list) List of allocated clusters.

See also: process(); get_centers(); get_total_wce()

Definition at line 314 of file xmeans.py.

Referenced by pyclustering.samples.answer_reader.get_cluster_lengths().

◆ get_total_wce()

def pyclustering.cluster.xmeans.xmeans.get_total_wce ( self )

Returns sum of Euclidean Squared metric errors (SSE - Sum of Squared Errors).

Sum of metric errors is calculated using distance between point and its center:

\[error=\sum_{i=0}^{N}euclidean_square_distance(x_{i}-center(x_{i}))\]

See also: process(); get_clusters()

Definition at line 357 of file xmeans.py.

◆ predict()

def pyclustering.cluster.xmeans.xmeans.predict	(	self,
		points
	)

Calculates the closest cluster to each point.

Parameters

[in] points (array_like): Points for which closest clusters are calculated.

Returns: (list) List of closest clusters for each point. Each cluster is denoted by index. Return empty collection if 'process()' method was not called.

An example how to calculate (or predict) the closest cluster to specified points.

from pyclustering.cluster.xmeans import xmeans
from pyclustering.samples.definitions import SIMPLE_SAMPLES
from pyclustering.utils import read_sample
 
# Load list of points for cluster analysis.
sample = read_sample(SIMPLE_SAMPLES.SAMPLE_SIMPLE3)
 
# Initial centers for sample 'Simple3'.
initial_centers = [[0.2, 0.1], [4.0, 1.0], [2.0, 2.0], [2.3, 3.9]]
 
# Create instance of X-Means algorithm with prepared centers.
xmeans_instance = xmeans(sample, initial_centers)
 
# Run cluster analysis.
xmeans_instance.process()
 
# Calculate the closest cluster to following two points.
points = [[0.25, 0.2], [2.5, 4.0]]
closest_clusters = xmeans_instance.predict(points)
print(closest_clusters)

Definition at line 264 of file xmeans.py.

◆ process()

def pyclustering.cluster.xmeans.xmeans.process ( self )

Performs cluster analysis in line with rules of X-Means algorithm.

Returns: (xmeans) Returns itself (X-Means instance).

See also: get_clusters(); get_centers()

Definition at line 206 of file xmeans.py.

Referenced by pyclustering.cluster.xmeans.xmeans.get_total_wce().

The documentation for this class was generated from the following file:

pyclustering/cluster/xmeans.py

Public Member Functions