pyclustering.nnet.hhn.hhn_network Class Reference

Oscillatory Neural Network with central element based on Hodgkin-Huxley neuron model. More...

Inheritance diagram for pyclustering.nnet.hhn.hhn_network:

Collaboration diagram for pyclustering.nnet.hhn.hhn_network:

Public Member Functions
def	__init__ (self, num_osc, stimulus=None, parameters=None, type_conn=None, type_conn_represent=conn_represent.MATRIX, ccore=True)
	Constructor of oscillatory network based on Hodgkin-Huxley neuron model. More...
def	__del__ (self)
	Destroy dynamically allocated oscillatory network instance in case of CCORE usage.
def	simulate (self, steps, time, solution=solve_type.RK4)
	Performs static simulation of oscillatory network based on Hodgkin-Huxley neuron model. More...
def	simulate_static (self, steps, time, solution=solve_type.RK4)
	Performs static simulation of oscillatory network based on Hodgkin-Huxley neuron model. More...
def	hnn_state (self, inputs, t, argv)
	Returns new values of excitatory and inhibitory parts of oscillator and potential of oscillator. More...
def	allocate_sync_ensembles (self, tolerance=0.1)
	Allocates clusters in line with ensembles of synchronous oscillators where each. More...
Public Member Functions inherited from pyclustering.nnet.network
def	height (self)
	Height of the network grid (that is defined by amout of oscillators in each column), this value is zero in case of non-grid structure. More...
def	width (self)
	Width of the network grid, this value is zero in case of non-grid structure. More...
def	structure (self)
	Type of network structure that is used for connecting oscillators.
def	__init__ (self, num_osc, type_conn=conn_type.ALL_TO_ALL, conn_repr=conn_represent.MATRIX, height=None, width=None)
	Constructor of the network. More...
def	__len__ (self)
	Returns size of the network that is defined by amount of oscillators.
def	has_connection (self, i, j)
	Returns True if there is connection between i and j oscillators and False - if connection doesn't exist. More...
def	set_connection (self, i, j)
	Couples two specified oscillators in the network with dynamic connections. More...
def	get_neighbors (self, index)
	Finds neighbors of the oscillator with specified index. More...

Detailed Description

Oscillatory Neural Network with central element based on Hodgkin-Huxley neuron model.

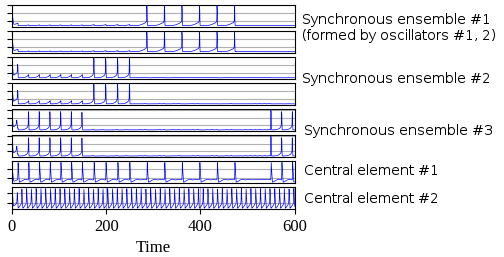
Interaction between oscillators is performed via central element (no connection between oscillators that are called as peripheral). Peripheral oscillators receive external stimulus. Central element consist of two oscillators: the first is used for synchronization some ensemble of oscillators and the second controls synchronization of the first central oscillator with various ensembles.

Usage example where oscillatory network with 6 oscillators is used for simulation. The first two oscillators have the same stimulus, as well as the third and fourth oscillators and the last two. Thus three synchronous ensembles are expected after simulation.

from pyclustering.nnet.hhn import hhn_network, hhn_parameters
from pyclustering.nnet.dynamic_visualizer import dynamic_visualizer

# Change period of time when high strength value of synaptic connection exists from CN2 to PN.
params = hhn_parameters()
params.deltah = 400

# Create Hodgkin-Huxley oscillatory network with stimulus.
net = hhn_network(6, [0, 0, 25, 25, 47, 47], params)

# Simulate network.
(t, dyn_peripheral, dyn_central) = net.simulate(2400, 600)

# Visualize network's output (membrane potential of peripheral and central neurons).
amount_canvases = 6 + 2  # 6 peripheral oscillator + 2 central elements
visualizer = dynamic_visualizer(amount_canvases, x_title="Time", y_title="V", y_labels=False)
visualizer.append_dynamics(t, dyn_peripheral, 0, True)
visualizer.append_dynamics(t, dyn_central, amount_canvases - 2, True)
visualizer.show()

There is visualized result of simulation where three synchronous ensembles of oscillators can be observed. The first and the second oscillators form the first ensemble, the third and the fourth form the second ensemble and the last two oscillators form the third ensemble.

Definition at line 168 of file hhn.py.

Constructor & Destructor Documentation

__init__()

def pyclustering.nnet.hhn.hhn_network.__init__	(		self,
			num_osc,
			stimulus = None,
			parameters = None,
			type_conn = None,
			type_conn_represent = conn_represent.MATRIX,
			ccore = True
	)

Constructor of oscillatory network based on Hodgkin-Huxley neuron model.

Parameters

[in]	num_osc	(uint): Number of peripheral oscillators in the network.
[in]	stimulus	(list): List of stimulus for oscillators, number of stimulus should be equal to number of peripheral oscillators.
[in]	parameters	(hhn_parameters): Parameters of the network.
[in]	type_conn	(conn_type): Type of connections between oscillators in the network (ignored for this type of network).
[in]	type_conn_represent	(conn_represent): Internal representation of connection in the network: matrix or list.
[in]	ccore	(bool): If 'True' then CCORE is used (C/C++ implementation of the model).

Definition at line 208 of file hhn.py.

Member Function Documentation

allocate_sync_ensembles()

def pyclustering.nnet.hhn.hhn_network.allocate_sync_ensembles	(		self,
			tolerance = 0.1
	)

Allocates clusters in line with ensembles of synchronous oscillators where each.

Synchronous ensemble corresponds to only one cluster.

Parameters

[in]

tolerance

(double): maximum error for allocation of synchronous ensemble oscillators.

Returns

(list) Grours (lists) of indexes of synchronous oscillators. For example [ [index_osc1, index_osc3], [index_osc2], [index_osc4, index_osc5] ].

Definition at line 552 of file hhn.py.

Referenced by pyclustering.gcolor.hysteresis.hysteresis_analyser.allocate_clusters(), pyclustering.cluster.syncnet.syncnet_analyser.allocate_clusters(), and pyclustering.gcolor.sync.syncgcolor_analyser.allocate_color_clusters().

hnn_state()

def pyclustering.nnet.hhn.hhn_network.hnn_state	(		self,
			inputs,
			t,
			argv
	)

Returns new values of excitatory and inhibitory parts of oscillator and potential of oscillator.

Parameters

[in]	inputs	(list): States of oscillator for integration [v, m, h, n] (see description below).
[in]	t	(double): Current time of simulation.
[in]	argv	(tuple): Extra arguments that are not used for integration - index of oscillator.

Returns

(list) new values of oscillator [v, m, h, n], where: v - membrane potantial of oscillator, m - activation conductance of the sodium channel, h - inactication conductance of the sodium channel, n - activation conductance of the potassium channel.

Definition at line 465 of file hhn.py.

Referenced by pyclustering.nnet.hhn.hhn_network.simulate_static().

simulate()

def pyclustering.nnet.hhn.hhn_network.simulate	(		self,
			steps,
			time,
			solution = solve_type.RK4
	)

Performs static simulation of oscillatory network based on Hodgkin-Huxley neuron model.

Output dynamic is sensible to amount of steps of simulation and solver of differential equation. Python implementation uses 'odeint' from 'scipy', CCORE uses classical RK4 and RFK45 methods, therefore in case of CCORE HHN (Hodgkin-Huxley network) amount of steps should be greater than in case of Python HHN.

Parameters

[in]	steps	(uint): Number steps of simulations during simulation.
[in]	time	(double): Time of simulation.
[in]	solution	(solve_type): Type of solver for differential equations.

Returns

(tuple) Dynamic of oscillatory network represented by (time, peripheral neurons dynamic, central elements dynamic), where types are (list, list, list).

Definition at line 266 of file hhn.py.

simulate_static()

def pyclustering.nnet.hhn.hhn_network.simulate_static	(		self,
			steps,
			time,
			solution = solve_type.RK4
	)

Performs static simulation of oscillatory network based on Hodgkin-Huxley neuron model.

Output dynamic is sensible to amount of steps of simulation and solver of differential equation. Python implementation uses 'odeint' from 'scipy', CCORE uses classical RK4 and RFK45 methods, therefore in case of CCORE HHN (Hodgkin-Huxley network) amount of steps should be greater than in case of Python HHN.

Parameters

[in]	steps	(uint): Number steps of simulations during simulation.
[in]	time	(double): Time of simulation.
[in]	solution	(solve_type): Type of solver for differential equations.

Returns

(tuple) Dynamic of oscillatory network represented by (time, peripheral neurons dynamic, central elements dynamic), where types are (list, list, list).

Definition at line 286 of file hhn.py.

Referenced by pyclustering.nnet.hhn.hhn_network.simulate(), pyclustering.nnet.hysteresis.hysteresis_network.simulate(), pyclustering.nnet.syncpr.syncpr.simulate(), and pyclustering.nnet.sync.sync_network.simulate().

---

The documentation for this class was generated from the following file:

• pyclustering/nnet/hhn.py