Class implements G-Means clustering algorithm. More...

Public Member Functions
def	__init__ (self, data, k_init=1, ccore=True, kwargs)
	Initializes G-Means algorithm. More...

def	process (self)
	Performs cluster analysis in line with rules of G-Means algorithm. More...

def	predict (self, points)
	Calculates the closest cluster to each point. More...

def	get_clusters (self)
	Returns list of allocated clusters, each cluster contains indexes of objects in list of data. More...

def	get_centers (self)
	Returns list of centers of allocated clusters. More...

def	get_total_wce (self)
	Returns sum of metric errors that depends on metric that was used for clustering (by default SSE - Sum of Squared Errors). More...

Detailed Description

Class implements G-Means clustering algorithm.

The G-means algorithm starts with a small number of centers, and grows the number of centers. Each iteration of the G-Means algorithm splits into two those centers whose data appear not to come from a Gaussian distribution. G-means repeatedly makes decisions based on a statistical test for the data assigned to each center.

Implementation based on the paper [17].

G-Means clustering results on most common data-sets.

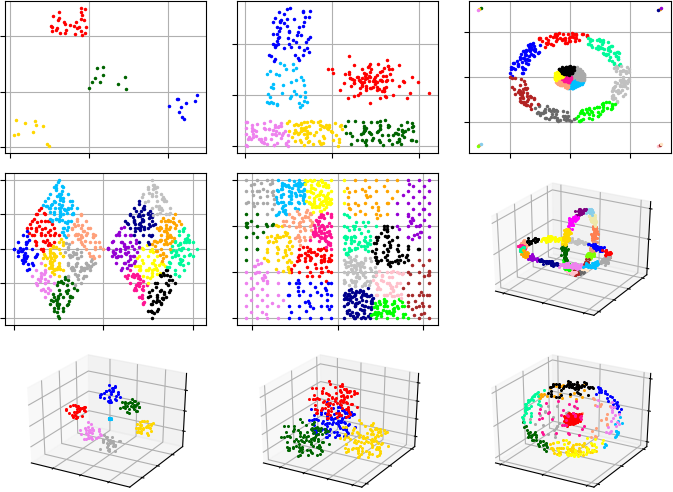
Example #1. In this example, G-Means starts analysis from single cluster.

from pyclustering.cluster import cluster_visualizer
from pyclustering.cluster.gmeans import gmeans
from pyclustering.utils import read_sample
from pyclustering.samples.definitions import FCPS_SAMPLES
# Read sample 'Lsun' from file.
sample = read_sample(FCPS_SAMPLES.SAMPLE_LSUN)
# Create instance of G-Means algorithm. By default the algorithm starts search from a single cluster.
gmeans_instance = gmeans(sample).process()
# Extract clustering results: clusters and their centers
clusters = gmeans_instance.get_clusters()
centers = gmeans_instance.get_centers()
# Print total sum of metric errors
print("Total WCE:", gmeans_instance.get_total_wce())
# Visualize clustering results
visualizer = cluster_visualizer()
visualizer.append_clusters(clusters, sample)
visualizer.show()

Example #2. Sometimes G-Means may found local optimum. 'repeat' value can be used to increase probability to find global optimum. Argument 'repeat' defines how many times K-Means clustering with K-Means++ initialization should be run to find optimal clusters.

# Read sample 'Tetra' from file.
sample = read_sample(FCPS_SAMPLES.SAMPLE_TETRA)
# Create instance of G-Means algorithm. By default algorithm start search from single cluster.
gmeans_instance = gmeans(sample, repeat=10).process()
# Extract clustering results: clusters and their centers
clusters = gmeans_instance.get_clusters()
# Visualize clustering results
visualizer = cluster_visualizer()
visualizer.append_clusters(clusters, sample)
visualizer.show()

Definition at line 39 of file gmeans.py.

Constructor & Destructor Documentation

◆ init()

def pyclustering.cluster.gmeans.gmeans.__init__	(	self,
		data,
		k_init = `1`,
		ccore = `True`,
		kwargs
	)

Initializes G-Means algorithm.

Parameters

[in]	data	(array_like): Input data that is presented as array of points (objects), each point should be represented by array_like data structure.
[in]	k_init	(uint): Initial amount of centers (by default started search from 1).
[in]	ccore	(bool): Defines whether CCORE library (C/C++ part of the library) should be used instead of Python code.
[in]	**kwargs	Arbitrary keyword arguments (available arguments: 'tolerance', 'repeat').

Keyword Args:

tolerance (double): tolerance (double): Stop condition for each K-Means iteration: if maximum value of change of centers of clusters is less than tolerance than algorithm will stop processing.
repeat (unit): How many times K-Means should be run to improve parameters (by default is 3). With larger 'repeat' values suggesting higher probability of finding global optimum.

Definition at line 98 of file gmeans.py.

Member Function Documentation

◆ get_centers()

def pyclustering.cluster.gmeans.gmeans.get_centers ( self )

Returns list of centers of allocated clusters.

Returns: (array_like) Allocated centers.

See also: process(); get_clusters()

Definition at line 212 of file gmeans.py.

◆ get_clusters()

def pyclustering.cluster.gmeans.gmeans.get_clusters ( self )

Returns list of allocated clusters, each cluster contains indexes of objects in list of data.

Returns: (array_like) Allocated clusters.

See also: process(); get_centers()

Definition at line 199 of file gmeans.py.

Referenced by pyclustering.samples.answer_reader.get_cluster_lengths(), and pyclustering.cluster.optics.optics.process().

◆ get_total_wce()

def pyclustering.cluster.gmeans.gmeans.get_total_wce ( self )

Returns sum of metric errors that depends on metric that was used for clustering (by default SSE - Sum of Squared Errors).

Sum of metric errors is calculated using distance between point and its center:

$error=\sum_{i=0}^{N}distance(x_{i}-center(x_{i}))$

See also: process(); get_clusters()

Definition at line 225 of file gmeans.py.

◆ predict()

def pyclustering.cluster.gmeans.gmeans.predict	(	self,
		points
	)

Calculates the closest cluster to each point.

Parameters

[in] points (array_like): Points for which closest clusters are calculated.

Returns: (list) List of closest clusters for each point. Each cluster is denoted by index. Return empty collection if 'process()' method was not called.

Definition at line 176 of file gmeans.py.

◆ process()

def pyclustering.cluster.gmeans.gmeans.process ( self )

Performs cluster analysis in line with rules of G-Means algorithm.

Returns: (gmeans) Returns itself (G-Means instance).

See also: get_clusters(); get_centers()

Definition at line 133 of file gmeans.py.

Referenced by pyclustering.cluster.gmeans.gmeans.get_total_wce().

The documentation for this class was generated from the following file:

pyclustering/cluster/gmeans.py

Public Member Functions